计算机体系结构与程序性能
2009-01-22 08:28 by 老赵, 14829 visits文章原来的题目是《计算机基础对.NET程序员是否重要》,再我看来,这是一句废话。
当然重要。可是好像有些朋友对于这点很疑惑。最近我又收到一封邮件,一个朋友问我说,他在大学里学的那些课程,似乎都无法对工作有所帮助——当然,这是他目前对于工作的观察,其中大部分是他通过博客园的“管中窥豹”得来的结果:
- 好多讲ASP.NET的文章啊,控件真好用,做网站很方便。
- ORM好像对开发很有帮助,我们也来LINQ to SQL,NHibernate一下……网站不就是CRUD吗?
- JavaScript框架XXX的效果好炫,网站越来越漂亮了。
- 好像进入并行处理时代了?呀,有了微软的并行库,加上AsParallel方法就能变快了。
- ……
(以上内容略有艺术夸张,如有雷同,绝非巧合)
是啊,看看大学里的那些课程:数据结构、算法、操作系统、网络、计算机组成原理、编译原理……工作中哪里用上了?于是乎,那位朋友说,他看不少同学平时不上课,也能做做几个网站赚点小钱,生活过的十分滋润。而自己却越学越迷茫,不知应该“转行”去“学做网站”,还是继续“好好学习,天天向上”。我给他的建议是:在大学就好好上课,珍惜学校里的宝贵时光,以免工作时候后悔;如果觉得老师课上得不好,那么就自己看教材,用心去看(不过老师上的好还是要靠自己课后钻研);如果嫌教材不好,那么去买点好教材,现在似乎各种“美国名校教材”都能找到,然后埋头学习便是。
企业抱怨毕业生不好,不是因为他们学了大学里没有用的东西,而是因为学好的人实在太少了。“大学的东西没有用”,大部分原因是没有学好。
想起自己以前也写过类似的文章,叫做《我们到底该怎么学技术?如何成为一个优秀的技术人员?》。老赵自己又看了一遍,发现有朋友对文章里的这么一句话有不同看法:“如果您不了解计算机体系结构,又如何能在Multi-CPU(Multi-Core)时代写出真正高效的应用程序呢?”。他认为这个“如果”(当然也包括文章里的其他“如果”)并不成立。所以老赵现在不谈“数据结构与算法如何有助于改善编程思维有什么改善”,或是“操作系统中线程调度、内存分页机制对于开发大型应用程序的参考价值”等“虚无缥缈”之物。在这篇文章里,我想通过两个直接的例子,来说明了解计算机体系结构对于提高程序性能有什么样的作用。
Locality
在描述何为Locality之前,我们先来看一个例子。例如,我们现在有一个二维数组:
static void Main(string[] args) { int n = 1 << 10; int[,] array = new int[n, n]; for (int x = 0; x < n; x++) { for (int y = 0; y < n; y++) { array[x, y] = x; } } ... }
我们要对这个1024 * 1024的二位数组中所有元素求和。那么我们会怎么写呢?先随手写一把:
static int SumA(int[,] array, int n) { int sum = 0; for (int y = 0; y < n; y++) { for (int x = 0; x < n; x++) { sum += array[x, y]; } } return sum; }
一个二重循环,遍历二维数组中每一个元素,相加,这也太容易了吧?是啊,不过我们还是可以“换种写法”的:
static int SumB(int[,] array, int n) { int sum = 0; for (int x = 0; x < n; x++) { for (int y = 0; y < n; y++) { sum += array[x, y]; } } return sum; }
仔细看看,有没有发现区别?没错,只是内层循环和外层循环的位置换了一下。这么做的意义何在?测试一下便知:
static void TestLocality(int[,] array, int n) { Stopwatch watch1 = new Stopwatch(); watch1.Start(); for (int i = 0; i < 100; i++) SumA(array, n); watch1.Stop(); Console.WriteLine("SumA: " + watch1.Elapsed); Stopwatch watch2 = new Stopwatch(); watch2.Start(); for (int i = 0; i < 100; i++) SumB(array, n); watch2.Stop(); Console.WriteLine("SumB: " + watch2.Elapsed); }
我们把两种加法各执行100次,看看结果:
SumA: 00:00:04.8116776 SumB: 00:00:00.8342202
第二种做法性能是第一种做法的将近5倍。这就是Locality的威力。
Locality(局部性,不知道该不该这么翻译),通俗地说,就是通过利用“缓存”来提高程序运行效率。缓存是计算机中无所不在的概念,这里先借用《Computer Systems: A Programmer's Perspective》(下文称为CSAPP)中的一幅图来简单说明一下:
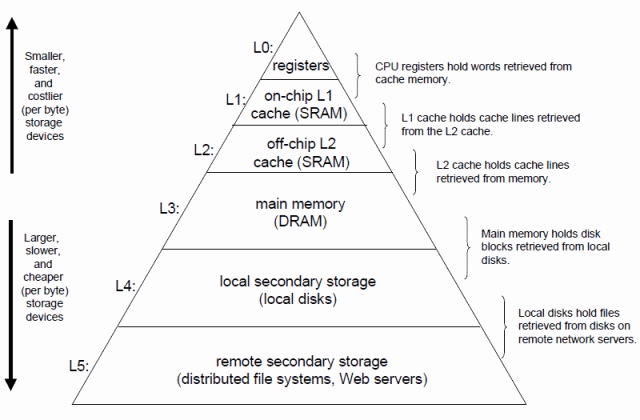
金字塔的每一层皆是“存储设备”,越靠近顶端则越速度越快,当然也越为昂贵。其中最快的当属寄存器,每个寄存器大小为一个字长(请问这是多大?),数量极其有限;L3则就是我们俗称的“内存”,大小……就取决于我们的荷包了;那么L1和L2是什么,大小又分别是多少呢?L1 Cache(又称Internal Cache),顾名思义它为CPU“内置”的缓存,速度次于寄存器,但还是远远高于内存。L2 Cache原本处于主板之上(因此又称External Cache),它比L1 Cache慢,速度也远高于内存,所以它做为CPU和Chips之间的缓冲——不过如今的CPU都已经“自带”L2 Cache,主板上自然就没有了。至于L1 Cache和L2 Cache的大小,您可以使用CPU-Z看看您机器CPU中Cache的情况如何。这是老赵的工作机:
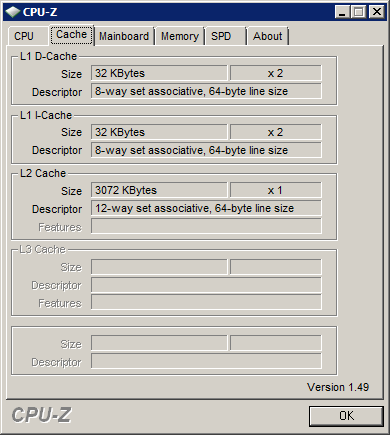
老赵的机器是双核,各有一个L1 Cache,分为L1 D-Cache(数据缓存)和L1 I-Cache(指令缓存),各32KB大小;两个核共用一个3MB大小的L2 Cache。Cache越大,CPU性能越高,这点毋庸置疑。
L1 Cache和L2 Cache的描述中都有“64-byte line size”字样,表示Cache的Line长为64字节。Line为Cache每次向下级存储设备读取数据的大小。例如,程序在运行时寄存器会向L1请求内存中某个地址的数据(可能是4字节),如果L1中没有这个地址的值,则会向L2中读取包含该地址的一整个Line的数据——也就是64字节,但是并不保证请求的4字节在这64字节的头部或尾部,CPU自有其对齐机制;如果L2没有这个地址的数据,则会向操作系统进行请求,同样是一个Line,64字节。
这就是Locality的关键。在系统中,一个好的Locality表现为,在读取某个地址之后的某个再次读取这个地址或者其附近的地址。由于在读取某个地址的数据之后,缓存中同样保留着附近地址的数据,因此如果请求临近的数据则速度就会非常快(L1 Cache无比迅速)。如果Locality很差,那么就会发现L1 Cache的失效率(Miss Ratio),甚至L2 Cache的失效率都会很高。如果CPU所需要的大量数据都要到L2 Cache甚至更为低效的内存中去读取(试想可能该次内存读取还需要从硬盘交换页上获得),那么性能不变差才令人奇怪。
说了不少“理论”,那么我们来看看上面的例子中为什么第一种方法会远远慢于第二种算法。我们的二维数组每个元素的下标(x, y)如下所示:
| 0, 0 | 0, 1 | 0, 2 | … | … | 0, 1021 | 0, 1022 | 0, 1023 |
| 1, 0 | |||||||
| 2, 0 | |||||||
| … | |||||||
| … | |||||||
| 1021, 0 | |||||||
| 1022, 0 | |||||||
| 1023, 0 | 1023, 1 | 1023, 2 | … | … | 1023, 1021 | 1023, 1022 | 1023, 1023 |
在内存中,每个元素的地址按照以下顺序次序排布:
(0, 0), (0, 1), (0, 2), …, (0, 1022), (0, 1023), (1, 0), (1, 1), …, (1023, 0), (1023, 1), …, (1023, 1022), (1023, 1023)
假如按照SumA方法中的读取顺序,L1 Cache中的状况可能就会是:
- 读取(0, 0)位置数据 => Cache Miss => L1向L2获取(0, 0), (0, 1), …, (0, 14), (0, 15)共64B数据 => 返回(0, 0)位置数据
- 读取(1, 0)位置数据 => Cache Miss => L1向L2获取(1, 0), (1, 1), …, (1, 14), (1, 15)共64B数据 => 返回(1, 0)位置数据
- ……
- 读取(1023, 0)位置数据 => Cache Miss => L1向L2获取(1023, 0), (1023, 1), …, (1023, 14), (1023, 15)共64B数据 => 返回(1023, 0)位置数据
- 读取(0, 1)位置数据 => Cache Miss(因为L1大小有限,读取(0, 0)时放入L1的64B数据已经被其他数据替换) => L1向L2获取(0, 0), (0, 1), …, (0, 14), (0, 15)共64B数据 => 返回(0, 1)位置数据
- 读取(1, 1)位置数据 => Cache Miss(理由同上) => L1向L2获取(1, 0), (1, 1), …, (1, 14), (1, 15)共64B数据 => 返回(1, 1)位置数据
- ……
而按照在SumB方法中的读取顺序,L1 Cache中的状况可能就会是:
- 读取(0, 0)位置数据 => Cache Miss => L1向L2获取(0, 0), (0, 1), …, (0, 14), (0, 15)共64B数据 => 返回(0, 0)位置数据
- 读取(0, 1)位置数据 => Cache Hit => 直接返回(0, 1)位置数据
- 读取(0, 2)位置数据 => Cache Hit => 直接返回(0, 2)位置数据
- ……
- 读取(1, 0)位置数据 => Cache Miss => L1向L2获取(1, 0), (1, 1), …, (1, 14), (1, 15)共64B数据 => 返回(1, 0)位置数据
- 读取(1, 1)位置数据 => Cache Hit => 直接返回返回(1, 1)位置数据
- ……
两种做法立分高下。
其实Locality这一特性在很多系统或应用中都有体现,例如磁盘文件的顺序读取就远比随机读取要快。再举个“时髦”点的东西,Google的Map Reduce论文中就使用了一节来提到Locality——调度器往往选择GFS中文件所在的机器作为Map Worker,这样可以通过读取本地文件尽可能减少数据在网络中的传输,从而大大提高效率。
False Sharing
尽可能读取接近的数据可以通过加强Locality来提高效率,但是在目前的多核甚至多CPU的环境下,操作两个“位置接近”数据可能反而会坏事。
再看一个例子。运行刚才的程序时您应该会发现CPU只用了50%左右,这是因为我们单线程的程序只能在一个核上运行。现在已经进入了并行时代,我们的程序也要与时俱进。微软推出了并行库让并行操作变得异常容易,那么我们就利用并行库来进行刚才二维数组所有元素求和。如下:
static int ParallelSumA(int[,] array, int n) { int processorCount = Environment.ProcessorCount; int[] result = new int[processorCount]; Parallel.For(0, processorCount, (part) => { int minInclusive = part * n / processorCount; int maxExclusive = minInclusive + n / processorCount; for (int x = minInclusive; x < maxExclusive; x++) { for (int y = 0; y < n; y++) { result[part] += array[x, y]; } } }); int sum = 0; for (int i = 0; i < result.Length; i++) { sum += result[i]; } return sum; }
我们首先获取系统中的处理器数目(processorCount),然后根据这个数据对二维数组进行分块,每个线程负责其中一块的计算,并将其保存到一个中间值中(result数组),最后再把所有的中间值累加即可。这种做法是并行计算中常用的模式,有了并行库的帮助,代码可以变得非常简单,直观。不过还是要用数据说话,还是100次求和运算,消耗时间为:
00:00:01.8105218
怎么所花时间反而比单线程要增加了!这固然有线程调度的开销在里面,但是问题的关键还是程序的写法有问题,这种写法发生了False Sharing。
False Sharing(错误共享)意为错误地共享了本不该共享的数据。由于每个核的L1缓存互相独立,因此CPU必须有一种机制,能够确保一个核在向它的L1 Cache中写入一个值之后,其他核内L1 Cache中包含这个数据的整个Line就会过期。这意味着其他核在读取地址相同,或者是接近的数据时会遇到L1 Cache Miss。CPU的这种同步机制就是MESI协议。那么我们来分析一下上面的代码到底如何造成了False Sharing。
上面的并行代码会将二维数组分割为独立的几块数据,并且将每一块数据之和存入result数组中。result数组很小,每次都会被完整地读入每个核的L1 Cache内,修改其中任何一个元素都会导致所有核内的result数据过期。于是,两个核在计算时可能就会发生如下情况(以下用CL0和CL1来代表两个核的L1缓存):
- CL0读取result[0]的值 => Cache Miss => result数组被加载到CL0中 => 修改CL0中result[0]
- CL1读取result[1]的值 => Cache Miss => result数组被加载到CL1中 => 修改CL1中result[1]
- CL0读取result[0]的值 => 由于刚才CL1修改了result[1],导致整条Line失效,于是Cache Miss => result数组被加载到CL0中 => 修改CL0中result[0]
- CL1读取result[1]的值 => 由于刚才CL0修改了result[0],导致整条Line失效,于是Cache Miss => result数组被加载到CL1中 => 修改CL0中result[1]
- ……
从此,两个核结下了不解之缘,他俩将会纠缠大部分时间,直到整个任务结束。当然,在上面的问题中,消除False Sharing非常容易:
static int ParallelSumB(int[,] array, int n) { int processorCount = Environment.ProcessorCount; int[] result = new int[processorCount]; Parallel.For(0, processorCount, (part) => { int partSum = 0; int minInclusive = part * n / processorCount; int maxExclusive = minInclusive + n / processorCount; for (int x = minInclusive; x < maxExclusive; x++) { for (int y = 0; y < n; y++) { partSum += array[x, y]; } } result[part] = partSum; }); int sum = 0; for (int i = 0; i < result.Length; i++) { sum += result[i]; } return sum;
与ParallelSumA方法的实现不同,ParallelSumB使用了一个临时变量partSum来保存每次元素相加后的结果,在最后才将partSum,也就是某一块数据计算后的最终结果写入result数组。由于partSum位于不同线程的堆栈上,因此不同线程的partSum变量的地址分布很广,很难被同时读入同一个核的L1 Cache中,自然也不会造成False Sharing。ParallelSumB方法的性能就会较为令人满意,它执行100次所花时间为:
00:00:00.5366263
上面的例子说明了一点:即使从代码角度来看没有共享任何数据,False Sharing还是可能发生。这迫使我们开发人员在平时工作中需要多留个心眼,偶尔也要考虑一下不同线程频繁修改的数据地址是否非常接近。这需要开发人员对一些“黑盒”内的状况进行适当探索。例如:在.NET程序中,由于托管堆内分配空间的连续性,几乎同时分配的对象地址会比较接近。而且,由于垃圾收集机制在回收时会进行“挤压”,因此生存时间久的对象的地址会愈发接近。可见,即使有了并行库,并行开发依旧不是那么容易。
回到这片文章的主题。不知道经过这两个示例,朋友们是否更进一步了解到计算机体系结构是如何对开发高性能应用程序,尤其是并行环境下的应用程序产生影响的。类似的事例还有很多,也欢迎您谈谈自己的感想。
广告时间
老赵还是要强调计算机基础课程的重要性,也因此在这里推广一个课程。这们课叫做ICS,全称叫做Introduction to Computer System,是老赵就读的复旦大学软件学院大二学生的必修课,由软件学院院长臧斌宇教授主讲。使用的教材便是之前提到的CSAPP。更为关键的是,这门课现在已经成为复旦大学的精品课程,其课件、作业、解答、甚至某些课程的录像也都会在网上公开。大家可以在http://ics.fudan.edu.cn/上访问该课程。
臧教授是老赵十分佩服的一位德才兼备的教授,还非常年轻。他的实验室在系统、编译、网格计算等方面成绩斐然,严谨的科研氛围也一直让我向往。老赵由他带出来的师兄师姐师弟师妹非常之牛,往往去国内其他科研机构发展的硕士生都会给那里的博士生带来很大压力。他们发布在顶级期刊上的论文不在少数(例如这次在OSDI08里就有他们的科研结果),也经常有人被美国名校录取。





刚好看到另一篇好文:
http://www.jdon.com/article/31338.html。